Zum Hauptinhalt springen
26P

2. Fehlerkorrektur

@

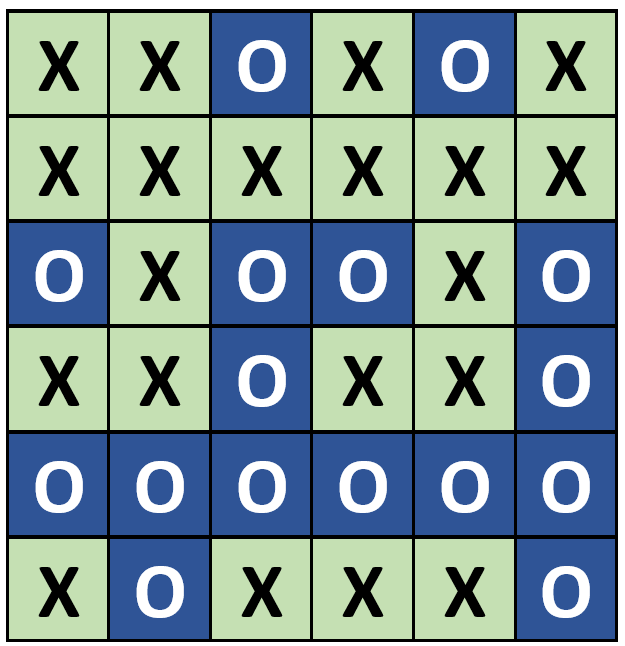
Im Unterricht haben Sie gesehen, wie die umgedrehte Karte sofort entdeckt wurde - Zauberei!?!?

Aufgaben

  1. Beschreiben Sie, nach welchem Prinzip Herr Hofer das 5x5-Muster zu einem 6x6-Muster ergänzt hat.

  2. Spielen Sie das XO-Spiel1 mit verschiedenen Mustern durch. Jede Spieler:in darf zweimal „raten“.

Von nun an soll das gelegte 6x6-Muster nicht mehr geändert werden.

  1. Überprüfen Sie, ob es eine Position in diesen 6x6-Muster gibt, bei der die Drehung einer Karte nicht erkannt wird.

  2. Zwei nebeneinander liegende Kärtchen werden umgedreht. Überprüfen Sie, ob der Fehler erkannt werden kann. Wenn ja, können Sie den Fehler auch korrigieren?

  3. Nun werden zwei beliebige Kärtchen umgedreht. Überprüfen Sie wieder, ob der Fehler erkannt und korrigiert werden kann.

  4. Geben Sie an, wie viele Möglichkeiten zur Korrektur gefunden werden können. Markieren Sie farbig (zusammengehörende Kärtchenpaare jeweils in einer Farbe) in den abgegebenen leeren 6x6-Raster diejenigen Positionen von Kärtchen, welche zur Korrektur in Frage kommen. Wiederholen Sie Aufgabe 5 noch zwei bis drei weitere Male und ergänzen Sie die Kästchen. Halten Sie Ihre Erkenntnisse mit einem Bild unten fest.

Paritätsprüfung (Paritätsbit)​

Eine Information soll binär codiert und anschliessend übertragen werden. Dabei soll erkannt werden, ob diese fehlerfrei übertragen wurde. Eine sehr einfache Methode zur Fehlererkennung bei binär codierten Informationen ist die Paritätsprüfung.

Dabei wird die Anzahl der Einsen der binär codierten Information gezählt:

  • Ist sie ungerade, wird an die Bitfolge eine „1“ angehängt, so dass die Anzahl der „Einsen“ gerade wird.

  • Ist sie gerade, wird an die Bitfolge eine „0“ angehängt, so dass die Anzahl der Einsen gerade bleibt.

Man spricht hierbei von einer geraden Parität. Das angehängte Bit wird Paritätsbit genannt.

Beispiel​

Binär codierte Information (7 Bit lang): 1000110

Zu übertragender Code mit Paritätsbit (7+1 Bit lang): 10001101

Das Paritätsbit ist hier 1.

Paritätsbit

Schreiben Sie mit Paritätsbit:

Sie erhalten 10 Bit-Sequenzen, wobei jede Sequenz mit einem Paritätsbit abgeschlossen ist.

10110100
11000011
11101011
01000011
11100001
11001010
11100100
01110011
11001010
11010010

Entfernen die fehlerhaft übertragenen Sequenzen und entfernen Sie alle Paritäts-Bits. Welche Nachricht wird angezeigt?

Binär Decodierer

Wieso wird ein p statt der Buchstabe b angezeigt? (b ist binär 1100010). Weshalb wurde dies nicht als Fehler erkannt?

EAN-13​

Letzthin beim Vorbereiten im Kaffee nebenan, wollte ich eine Packung Kaffee kaufen - doch das Einscannen des Codes ging nicht, so dass der Strichcode einer anderen Packung eingelesen werden musste...

Doch wie funktioniert das? Weshalb wurde erkannt, dass der Code kaputt war?

Nach einer kurzen Recherche: Die Strichcodes auf Verpackungen sind sog. EAN-13-Codes (EAN = European Article Number). Doch wie funktionieren diese?

EAN 13
EAN 13
Aufgabe

  1. Was könnte passieren, wenn ein Strichcode verdreckt oder beschädigt ist?

  2. Die ersten 12 Stellen des (richtigen) EAN-13 Codes der Baslercafé Verpackung lautet: 7610 4430 0204. Wie berechnet sich daraus nun die letzte Stelle, die Prüfziffer? Erkennen Sie das System? (Einfachheitshalber wurde eine weitere EAN-Nummer abgedruckt 4260 0806 8005).

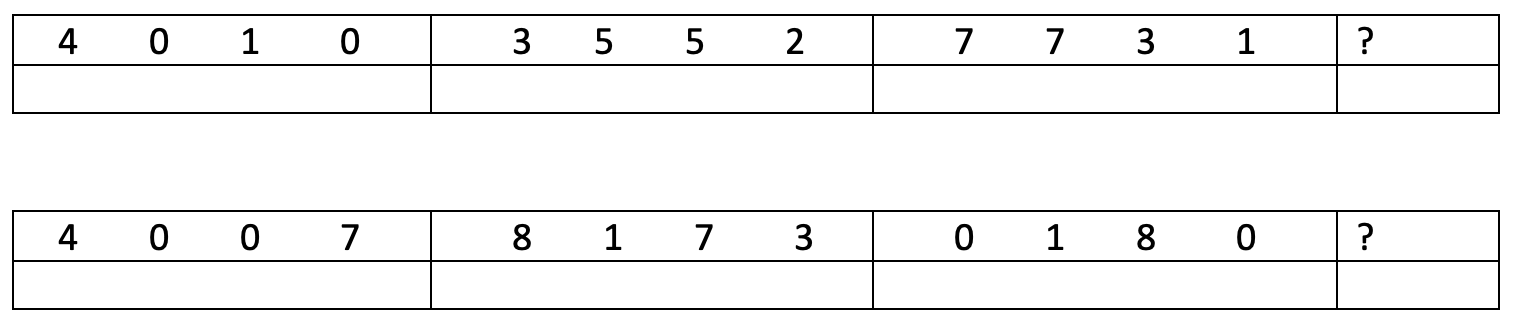
    • Führen Sie zu diesen Codierungen die beiden untenstehende Rechnungen aus und halten Sie die Ergebnisse fest.

    • Ermitteln Sie anhand der beiden Beispiele, wie die letzte Ziffer mit der Rechnung zusammenhängt und beschreiben Sie das gefundene Verfahren.

  3. Berechnen Sie auch für die folgenden Strichcodes die Prüfziffer:

Footnotes​

  1. Inspirationsquelle: lehrerfortbildung-bw.de

    ↩
CC 4.0